পিথাগোরাসের উপপাদ্য প্রমান কর

সমকোণী ত্রিভুজের অতিভুজের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের ক্ষেত্রফলের সমষ্টির সমান।
পিথাগোরাসের উপপাদ্য: সমকোণী ত্রিভুজের অতিভুজের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের ক্ষেত্রফলের সমষ্টির সমান।
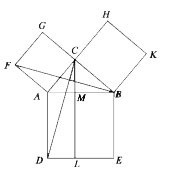
বিশেষ নির্বচন: মনে করি, ABC সমকোণী ত্রিভুজের ZACB সমকোণ এবং AB অতিভুজ। প্রমাণ করতে হবে যে, AB2 = BC2 + AC2
অঙ্কন: AB, AC এবং BC বাহুর উপর যথাক্রমে ABED, ACGF এবং BCHK বর্গক্ষেত্র অঙ্কন করি। C বিন্দু দিয়ে AD বা BE রেখার সমান্তরাল CL রেখা আঁকি। মনে করি, তা AB কে M বিন্দুতে এবং DE কে L বিন্দুতে ছেদ করে। C ও D এবং B ওF যোগ করি।
প্রমাণ:
ধাপ ১. ∇CAD ও ∇ABAF তে CA = AF, AD = AB এবং অন্তর্ভুক্ত∠CAD = ∠CAB + ∠BAD = ∠CAB + ∠CAF = অন্তর্ভুক্ত ∠BAF [ZBAD = ZCAF = 1 সমকোণ] অতএব, ∠CAD ∠BAF
ধাপ ২. ∠CAD এবং আয়তক্ষেত্র ADLM একই ভূমি AD এর উপর এবং AD ও CL সমান্তরাল রেখাদ্বয়ের মধ্যে অবস্থিত।
সুতরাং আয়তক্ষেত্র ADLM = 2 ∇CAD [উপপাদ্য ৩৭]
ধাপ ৩. ∠BAF এবং বর্গক্ষেত্র ACGF একই ভূমি AF এর উপর এবং AF ও BG সমান্তরাল রেখাদ্বয়ের মধ্যে অবস্থিত।
সুতরাং বর্গক্ষেত্র ACGF = ∇AFAB = 2∇CAD [উপপাদ্য ৩৭]
ধাপ ৪. আয়তক্ষেত্র ADLM = বর্গক্ষেত্র ACGF
ধাপ ৫. অনুরূপভাবে C, E ও A, Kযোগ করে প্রমাণ করা যায় যে,
আয়তক্ষেত্র BELM = বর্গক্ষেত্র BCHK
ধাপ ৬. আয়তক্ষেত্র (ADLM + BELM) = বর্গক্ষেত্র ACGF+ বর্গক্ষেত্র BCHK
বা, বর্গক্ষেত্র ABED = বর্গক্ষেত্র ACGF+ বর্গক্ষেত্র BCHK
অর্থাৎ, AB2 = BC2 + AC2 (প্রমাণিত)
পিথাগোরাসের উপপাদ্য